Operations and Algebraic Thinking
Represent and solve problems involving multiplication and division
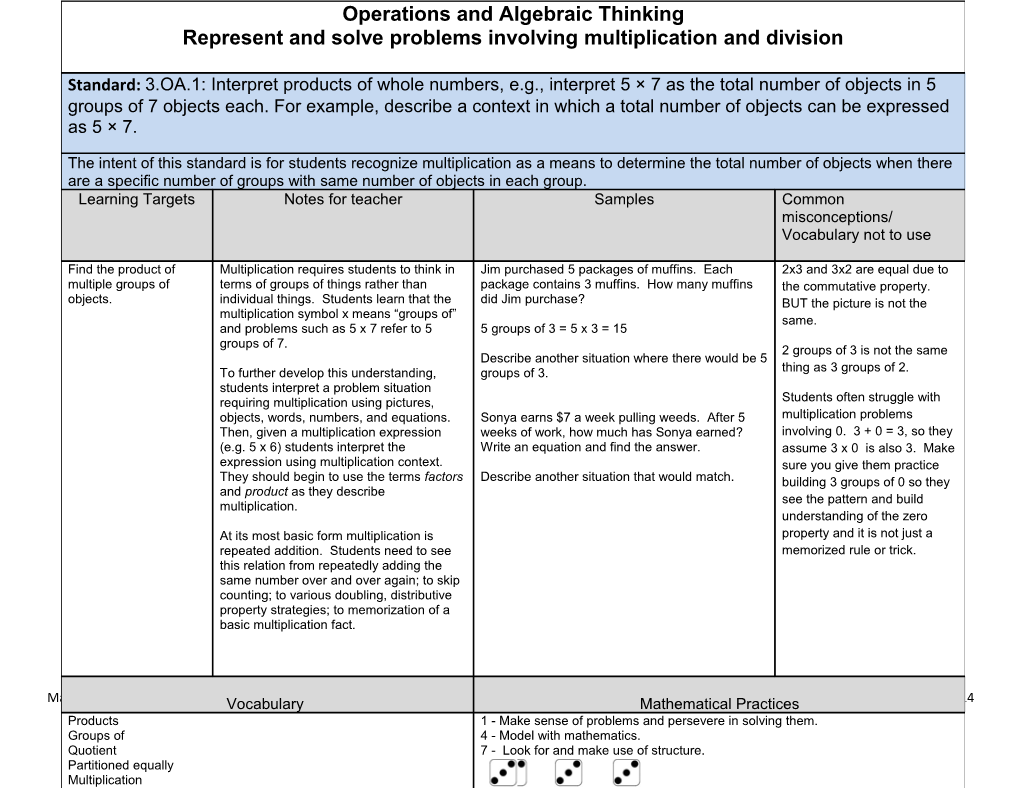
Standard: 3.OA.1: Interpret products of whole numbers, e.g., interpret 5 × 7 as the total number of objects in 5 groups of 7 objects each. For example, describe a context in which a total number of objects can be expressed as 5 × 7.
The intent of this standard is for students recognize multiplication as a means to determine the total number of objects when there are a specific number of groups with same number of objects in each group.
Learning Targets / Notes for teacher / Samples / Common misconceptions/ Vocabulary not to use
Find the product of multiple groups of objects. / Multiplication requires students to think in terms of groups of things rather than individual things. Students learn that the multiplication symbol x means “groups of” and problems such as 5 x 7 refer to 5 groups of 7.
To further develop this understanding, students interpret a problem situation requiring multiplication using pictures, objects, words, numbers, and equations. Then, given a multiplication expression (e.g. 5 x 6) students interpret the expression using multiplication context. They should begin to use the terms factors and product as they describe multiplication.
At its most basic form multiplication is repeated addition. Students need to see this relation from repeatedly adding the same number over and over again; to skip counting; to various doubling, distributive property strategies; to memorization of a basic multiplication fact. / Jim purchased 5 packages of muffins. Each package contains 3 muffins. How many muffins did Jim purchase?
5 groups of 3 = 5 x 3 = 15
Describe another situation where there would be 5 groups of 3.
Sonya earns $7 a week pulling weeds. After 5 weeks of work, how much has Sonya earned? Write an equation and find the answer.
Describe another situation that would match. / 2x3 and 3x2 are equal due to the commutative property. BUT the picture is not the same.
2 groups of 3 is not the same thing as 3 groups of 2.
Students often struggle with multiplication problems involving 0. 3 + 0 = 3, so they assume 3 x 0 is also 3. Make sure you give them practice building 3 groups of 0 so they see the pattern and build understanding of the zero property and it is not just a memorized rule or trick.
Vocabulary / Mathematical Practices
Products
Groups of
Quotient
Partitioned equally
Multiplication
Division
Equal groups
Group size
Arrays
Equations
Unknown
Expression
Per (ex. 3 boxes with 8 books per box. How many books?) / 1 - Make sense of problems and persevere in solving them.
4 - Model with mathematics.
7 - Look for and make use of structure.
Resources
Operations and Algebraic Thinking
Represent and solve problems involving multiplication and division.
Standard: 3.OA.2:
Interpret whole-number quotients of whole numbers, e.g., interpret 56 ÷ 8 as the number of objects in each share when 56 objects are partitioned equally into 8 shares, or as a number of shares when 56 objects are partitioned into equal shares of 8 objects each. For example, describe a context in which a number of shares or a number of groups can be expressed as 56 ÷ 8.
The intent of this standard is for students to understand and develop division number sense.
Learning Targets / Notes for teacher / Samples / Common misconceptions/ Vocabulary not to use
Explain what the numbers in a division problem mean.
Explain how division relates to multiplication and equal shares.
Identify quotients as the number of objects in each share or the number of equal shares. / 3.OA.2 focuses on two distinct models of division: partition models and measurement (repeated subtraction) models.
Partition models focus on the question – How many in each group?
Measurement (repeated subtraction) models focus on the question – How many groups can you make? / This standard focuses on two distinct models of division: partition models and measurement (repeated subtraction) models.
Partition models provide students with a total number and the number of groups. These models focus on the question, “How many objects are in each group so that the groups are equal?” A context for partition models would be: There are 12 cookies on the counter. If you are sharing the cookies equally among three bags, how many cookies will go in each bag?
Measurement (repeated subtraction) models provide students with a total number and the number of objects in each group. These models focus on the question, “How many equal groups can you make?” A context for measurement models would be: There are 12 cookies on the counter. If you put 3 cookies in each bag, how many bags will you fill?
/ Students do not think that the order in a division problem matters.
Ex. 8 divided by 56 = 7.
Vocabulary / Mathematical Practices
Products
Groups of
Quotient
Partitioned equally
Multiplication
Division
Equal groups
Group size
Arrays
Equations
Unknown
Expression
Per (ex. 3 boxes with 8 books per box. How many books?) / 1 - Make sense of problems and persevere in solving them.
4 - Model with mathematics.
7 - Look for and make use of structure.
Resources
Operations and Algebraic Thinking
Represent and solve problems involving multiplication and division.
Standard: 3.OA.3:
Use multiplication and division within 100 to solve word problems in situations involving equal groups, arrays, and measurement quantities, e.g., by using drawings and equations with a symbol for the unknown number to represent the problem. (Note: See Glossary, Table 2.)
The intent of this standard is for students to apply various problem solving strategies in different contexts.
Learning Targets / Notes for teacher / Samples / Common misconceptions/ Vocabulary not to use
Multiply and divide within 100.
Solve word problems in situations involving equal groups, arrays, and measurement quantities.
Represent a word problem using a picture, an equation with a symbol for the unknown number, or in other ways. / Students should apply their skills to solve word problems. This could include one or two-step word problems, such as:
In third grade students should use a variety of pictures, such as stars, boxes, flowers to represent unknown numbers (variables). Letters are also introduced to represent unknowns in third grade.
Various strategies that can be used to solve word problems involving multiplication and division.
However, THERE is a PROGRESSION of efficient strategies and you do not want your students to still be drawing individual flowers and counting by 1 at the end of the year to answer word problems. Be very aware as you try to move them from skip counting, to making arrays, and then to the open area model that students continue to build more efficient multiplication strategies. / 1) If you divide 4 dozen brownies among 8 people, how many cookies does each person receive? (4x12 = 48, 48 ÷ 8 = 6).
2) There are 24 desks in the classroom. If the teacher puts 6 desks in each row, how many rows are there?
This task can be solved by drawing an array by putting 6 desks in each row.
This task can also be solved by drawing pictures.
4 groups of 6 equals 24 objects
A student could also reason through the problem mentally or verbally, ―I know 6 and 6 are 12. 12 and 12 are 24. Therefore, there are 4 groups of 6 giving a total of 24 desks in the classroom.
3) There are some students at recess. The teacher divides the class into 4 lines with 6 students in each line. Write a division equation for this story and determine how many students are in the class ( ? divided by 4 = 6---- there are 24 students in the class).
…………………………………………………………………………………………………………..
Word problems may be represented in multiple ways:
• Equations: 3 x 4 = ?, 4 x 3 = ?, 12 ÷ 4 = ? and 12 ÷ 3 = ?
• Array
• Equal groups
• Repeated addition: 4 + 4 + 4 or repeated subtraction
• Three equal jumps forward from 0 on the number line to 12 or three equal jumps backwards from 12 to 0
Examples of division problems:
*Determining the number of objects in each share (partitive division, where the size of the groups is unknown):
o The bag has 92 hair clips, and Laura and her three friends want to share them equally. How many hair clips will each person receive?
*Determining the number of shares (measurement division, where the number of groups is unknown)
Starting / Day 1 / Day 2 / Day 3 / Day 4 / Day 5 / Day 6
24 / 24-4=20 / 20-4=16 / 16-4=12 / 12-4=8 / 8-4=4 / 4-4=0
Max the monkey loves bananas. Molly, his trainer, has 24 bananas. If she gives Max 4 bananas each day, how many days will the bananas last?
Solution: The bananas will last for 6 days.
Students may use interactive whiteboards to show work and justify their thinking.
Vocabulary / Mathematical Practices
Area model
Array
Divide
Dividend
Division
Divisor
Factor
Multiple
Multiplication
Multiply
Product
Quotient / 1 - Make sense of problems and persevere in solving them.
4 - Model with mathematics.
7 - Look for and make use of structure.
Resources
Operations and Algebraic Thinking
Represent and solve problems involving multiplication and division.
Standard: 3.OA.4: Determine the unknown whole number in a multiplication or division equation relating three whole numbers. For example, determine the unknown number that makes the equation true in each of the equations 8× ? = 48, 5 = 15 ÷ 3, 6 × 6 = ?.
The intent of this standard is for students to determine the missing value in multiplication and division problems that resemble these equations:
o m × n = ______× n = p m × __ = p (where m, n, and p are given values)
o m ÷ n = ______÷ n = q m ÷ __ = q (where m, n, and q are given values).
NOTE: The unknown value can be represented by a blank, empty box, question mark, or some other symbol.
Learning Targets / Notes for teacher / Samples / Common misconceptions/ Vocabulary not to use
Multiply and divide within 100.
Solve word problems in situations involving equal groups, arrays, and measurement quantities.
Represent a word problem using a picture, an equation with a symbol for the unknown number, or in other ways. / 3. OA.4 refers to Glossary, Table 2 and equations for the different types of multiplication and division problem structures.
The focus of 3.OA.4 goes beyond the traditional notion of fact families, by having students explore the inverse relationship of multiplication and division.
This standard is strongly connected to 3.OA.3 when students solve problems and determine unknowns in equations. Students should also experience creating story problems for given equations. When crafting story problems, they should carefully consider the question(s) to be asked and answered to write an appropriate equation. Students may approach the same story problem differently and write either a multiplication equation or division equation. / The easiest problem structure includes Unknown Product (3 x ? = 18 or 18 ÷ 3 = 6). The more difficult problem structures include Group Size Unknown (3 x ? = 18 or 18 ÷ 3 = 6) or Number of Groups Unknown (? x 6 = 18, 18 ÷ 6 = 3).
Students apply their understanding of the meaning of the equal sign as ”the same as” to interpret an equation with an unknown. When given 4 x ? = 40, they might think:
• 4 groups of some number is the same as 40
• 4 times some number is the same as 40
• I know that 4 groups of 10 is 40 so the unknown number is 10
• The missing factor is 10 because 4 times 10 equals 40.
Equations in the form of a x b = c and c = a x b should be used interchangeably, with the unknown in different positions.
Examples:
• Solve the equations below:
24 = ? x 6
9÷72=Δ
• Rachel has 3 bags. There are 4 marbles in each bag. How many marbles does Rachel have altogether? 3 x 4 = m. / The equal sign means “the same amount as.”
Some students struggle with equations where the product or quotient are written first in an equation.
Also be sure to give them practice where the unknown quantity is in various placements in the equation.
Vocabulary / Mathematical Practices
Area model
Array
Divide
Dividend
Division
Divisor
Factor
Multiple
Multiplication
Multiply
Product
Quotient / 1 - Make sense of problems and persevere in solving them.
2 - Reason abstractly and quantitatively.
4 - Model with mathematics.
6 - Attend to precision
7 - Look for and make use of structure.
Resources
Operations and Algebraic Thinking
Understand properties of multiplication and the relationship between multiplication and division.
Standard: 3.OA.5: Apply properties of operations as strategies to multiply and divide. (Note: Students need not use formal terms for these properties.) Examples: If 6 × 4 = 24 is known, then 4 × 6 = 24 is also known. (Commutative property of multiplication.) 3 × 5 × 2 can be found by 3 × 5 = 15, then 15 × 2 = 30, or by 5 × 2 = 10, then 3 × 10 = 30.(Associative property of multiplication.) Knowing that 8 × 5 = 40 and 8 × 2 = 16, one can find 8 × 7 as 8 × (5 + 2) = (8 × 5) + (8 × 2)= 40 + 16 = 56. (Distributive property.)
The intent of this standard is for students to develop an understanding of multiplication properties and be able to apply them to help them solve multiplication problems.
Learning Targets / Notes for teacher / Samples / Common misconceptions/ Vocabulary not to use
Multiply and divide within 100.
Split a number apart into smaller chucks to make it easier to multiply. (Distributive Property)
Rearrange the order of numbers I am multiplying to make it easier to mentally / 3.OA.5 references properties of multiplication. While students DO NOT need to not use the formal terms of these properties, student should understand that properties are rules about how numbers work, they need to be flexibly and fluently applying each of them.
Madison County Schools Spring 2014