Chapter 1
1.1 Physics: the Laws of Nature
1.2 Units of Length, Mass, and Time
1.3 Dimensional Analysis
1.4 Significant Figures & Uncertainty / 1.5 Conversion of Units
1.6 Order of Magnitude Calculations
1.7 Scalars & Vectors
1.1 Physics: the Laws of Nature
The study of the fundamental laws of nature and these laws can be expressed as mathematical equations.
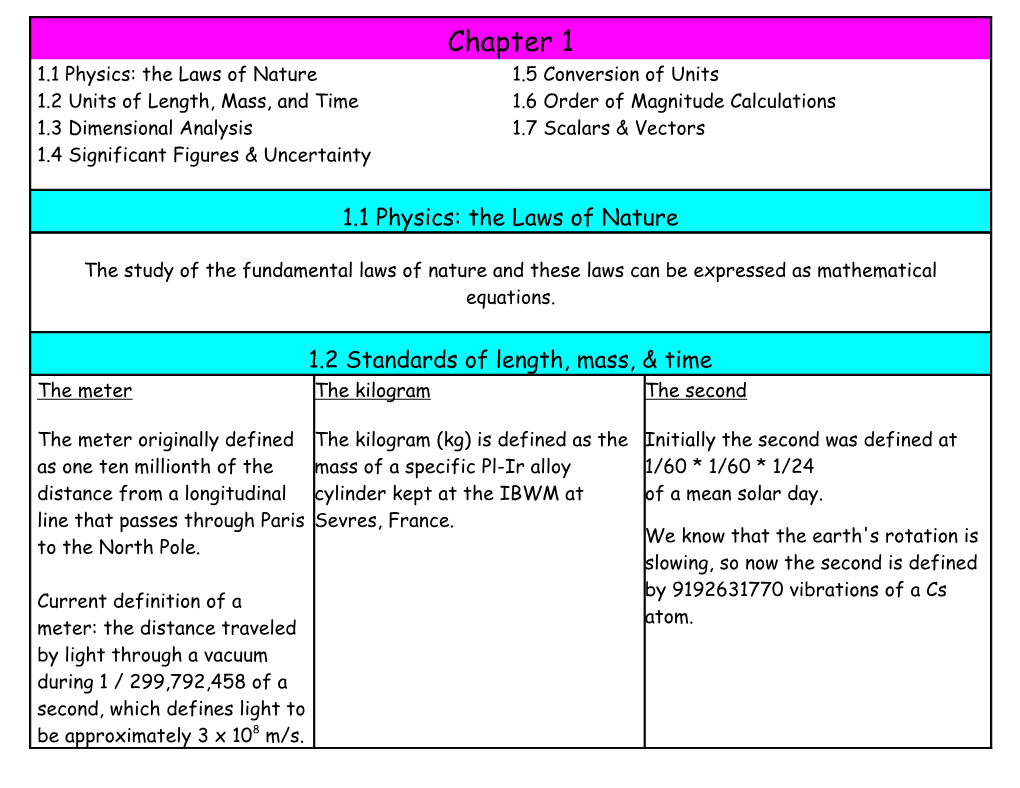
1.2 Standards of length, mass, & time
The meter
The meter originally defined as one ten millionth of the distance from a longitudinal line that passes through Paris to the North Pole.
Current definition of a meter: the distance traveled by light through a vacuum during 1 / 299,792,458 of a second, which defines light to be approximately 3 x 108 m/s. / The kilogram
The kilogram (kg) is defined as the mass of a specific Pl-Ir alloy cylinder kept at the IBWM at Sevres, France.
/ The second
Initially the second was defined at
1/60 * 1/60 * 1/24
of a mean solar day.
We know that the earth's rotation is slowing, so now the second is defined by 9192631770 vibrations of a Cs atom.
Demo: Standard Units of Measurement: ME-A-SU
Demo: Volume Comparison: ME-A-VC cc’s from 1 g/cc from meters
1.3 Dimensional Analysis & 1.5 Conversion of Units
You are driving along the highway with you speed of 60 mph. So the units of speed is miles / hour
· Speed à miles / hour
· Speed à meters / sec
* New Formula *
speed = distance / time
So is it possible for the units of speed to be m/s2?
m / s ≠ m / s2
So this is an impossibility / You are at a red traffic light. The light turns green. What do you do?
Ans: You step on the accelerator (or gas pedal).
See table to the right à
If you notice the Δspeed per unit time is constant
Δ is read as “change of”
* New Formula *
acceleration = Δvelocity / Δtime / The accelerator increases speed per unit time.
0 to 1 sec: 0 to 5 mph
1 to 2 sec: 5 to 10 mph
2 to 3 sec: 10 to 15 mph
3 to 4 sec: 15 to 20 mph
4 to 5 sec: 20 to 25 mph
In lecture we discuss the difference between speed (a magnitude) and speed with direction (magnitude w/direction).
Velocity is speed with direction which is a vector quantity
You are driving along the highway with you speed of 60 mph. Let’s convert this to miles per hour using estimations.
60 / miles / (1 hour) / (5280 ft) / (1 meter) / ≈ 30 m/s
hour / (3600 sec) / (1 mile) / (3.3 ft)
or 2 mph ≈ 1 m/s
As you can see…these are rough approximations. In reality there is about 2.2 mph = 1.0 m/s
But the IMPORTANT key to recognize…these calculations are easily completed…no calculator is needed !
1.4 Sig Figs and Uncertainty (Sig Figures from book)
When to use Significant Figures?
When accuracy of measurements is limited
· significant figures: the number of digits in a quantity that are known with certainty
· number of significant figures after multiplication or division is the number of significant figures in the least-known quantity / Example: A tortoise travels at 2.51 cm/s for 12.23 s. How far does the tortoise go?
Answer: 2.51 cm/s (12.23 s) = 30.7 cm
Uncertainty
· Always reported as absolute uncertainty
· NEVER show fractional uncertainty in a decimal form (looks like absolute uncertainty)
· Rules below w/ examples
a = 10 ± 1 / b = 2.0 ± 0.3 / c = 3.0 ± 0.1
Uncertainty that is added or subtracted: ABSOLUTE uncertainty is added
a + b = (10 ± 1) + (2.0 ± 0.3)
= 10 + 2.0 ± (1 + .3)
= 12 ± 1.3
a + b = 12 ± 1 / a – b = (10 ± 1) - (2.0 ± 0.3)
= 10 – 2.0 ± (1 + .3)
= 8.0 ± 1.3
a - b = 8 ± 1
Uncertainty that is multiplied or divided: FRACTIONAL (or percent) uncertainty is added
At this point we must convert the absolute uncertainty to Fractional
a * b = (10 ± 1) * (2.0 ± 0.3)
= (10 ± 1/10) * (2.0 ± 0.3/2)
= 10 * 2 ± (1/10 + 0.3/2)
= 20 ± (10% + 15%)
= 20 ± 25%
= 20 ± 25% * 20 ------> Converting back to ABSOLUTE
= 20 ± 5 / a / b = (10 ± 1) / (2.0 ± 0.3)
= (10 ± 1/10) / (2.0 ± 0.3/2)
= (10 ± 10%) / (2.0 ± 15%)
= 10 / 2 ± (10% + 15%)
= 5 ± 25%
= 5 ± 25% * 5 ------> Converting back to ABSOLUTE
= 5 ± 1.25
= 5 ± 1 (Follow one sig fig rule)
Uncertainty that is raised to a power: FRACTIONAL (or percent) uncertainty is multiplied by that power
a2 = (10 ± 1)2
= (10 ± 1/10)2
= (10 ± 10%)2
= 102 ± 10% * 2
= 100 ± 20%
= 100 ± (20% * 100)
= 100 ± 20 / a1/2 = (10 ± 1)½
= (10 ± 1/10)½
= (10 ± 10%)½
= 10½ ± (10% * ½)
= 3.2 ± 5%
= 3.2 ± (5% * 3.2)
= 3.2 ± 0.2
a * b + c
= (10 ± 1) * (2.0 ± 0.3) + 3.0 ± 0.1
= (10 ± 1/10) * (2.0 ± 0.3/2) + 3.0 ± 0.1
= (10 ± 10%) * (2.0 ± 15%) + 3.0 ± 0.1
= 20 ± 25% + 3.0 ± 0.1
= 20 ± 25% * 20 + 3.0 ± 0.1
= 20 ± 5 + 3.0 ± 0.1
= 20 + 3 ± (5 + 0.1)
= 23 ± 5.1 (but uncertainty must be to same decimal place)
= 23 ± 5
or 20.3 ± 5.1 (I prefer…but doesn’t follow 1 sig fig for uncertainty rule) / a / b - c
= (10 ± 1) / (2.0 ± 0.3) - 3.0 ± 0.1
= (10 ± 1/10) / (2.0 ± 0.3/2) - 3.0 ± 0.1
= (10 ± 10%) / (2.0 ± 15%) - 3.0 ± 0.1
= 5 ± 25% - 3.0 ± 0.1
= 5 ± 25% * 5 - 3.0 ± 0.1
= 5 ± 1.25 - 3.0 ± 0.1
= 5 – 3.0 ± (1.25 + 0.1)
= 2 ± 1.35
= 2 ± 1
or 2.0 ± 1.4 (I prefer…but doesn’t follow 1 sig fig for uncertainty rule)
a3 * b / c
= (10 ± 1)3 * (2.0 ± 0.3) / 3.0 ± 0.1
= (1000 ± 3(1/10)) * (2.0 ± 0.3/2) / 3.0 ± 0.1/3
= (1000 ± 3(10%)) * (2.0 ± 15%) / 3.0 ± 3.33%
= 1000 * 2 / 3 ± (30% + 15% + 3.33%)
= 667 ± 48.3%
= 667 ± 48.3% * 667
= 667 ± 322
= 667 ± 330 or Remember…I prefer 2 sig figs for uncertainty…but rule states
= 700 ± 400 you can only have one sig fig for uncertainty
One last uncertainty problem
a3 * b / c - (a – b)
= (10 ± 1)3 * (2.0 ± 0.3) / 3.0 ± 0.1 - [10 ± 1) - (2.0 ± 0.3]
= (1000 ± 3(1/10)) * (2.0 ± 0.3/2) / 3.0 ± 0.1/3 - [10 - 2 ± (1 + .3)]
= (1000 ± 3(10%)) * (2.0 ± 15%) / 3.0 ± 3.33% - (8 ± 1.3)
= 1000 * 2 / 3 ± (30% + 15% + 3.33%) - (8 ± 1.3)
= 667 ± 48.3% - (8 ± 1.3)
= 667 ± 48.3% * 667 - (8 ± 1.3)
= 667 ± 322 - (8 ± 1.3)
= (667 – 8) ± (322 + 1.3)
= 659 ± 323
= 660 ± 330 (I prefer this)
= 700 ± 400 (Standard recognized correct answer)
So the real value falls somewhere between 300 to 1100 (quite a big range)
Another uncertainty problem
4 / a(1/2) * ( a * b - b / c)
= 4 /(10 ± 1)1/2 * (10 ± 1 * 2.0 ± 0.3 - 2.0 ± 0.3 / 3.0 ± 0.1)
= 4 / 3.32 ± (½*1/10) * (20 ± (1/10 + 0.3/2.0) - 0.667 ± (0.3/2 + 0.1/3))
= 1.20 ± 5% * (20 ± (10% + 15%) - 0.667 ± (15% + 3.33%))
= 1.20 ± 5% * (20 ± 25% - 0.667 ± 18.33%)
= 1.20 ± 5% * (20 ± 5 - 0.667 ± 0.122)
= 1.20 ± 5% * (19.33 ± 5.12)
= 1.20 ± 5% * (19.33 ± 5.12/19.33)
= 1.20 ± 5% * (19.33 ± 26.5%)
= 24.5 ± 31.5%
= 24.5 ± 7.7 (I prefer this)
= 25 ± 8 (Standard recognized correct answer)
1.6 Order of Magnitude Calculations
Why are estimates useful?
· a check for a detailed calculation –
1. if your answer is very different from your estimate, you’ve probably made an error
· to estimate numbers where a precise calculation cannot be done
1.7 Scalars & Vectors
One day you decide to drive your car for 1 hour. There is no traffic and you drive at a speed of 65 miles per hour. Where are you?
You can easily determine you have traveled about 65 miles. But which direction? / SCALAR: 65 miles is a scalar. This is just a magnitude of a value, no direction is given.
You must also know which direction to know you final location.
VECTOR: A magnitude WITH a direction is called a vector.
Boddeker's Mechanics Notes